Use Our NMR service for all your NMR needs.

Uses of NMR spectroscopy

Nuclear Magnetic Resonance (NMR) spectroscopy is an analytical chemistry technique used in quality control and research for determining the content and purity of a sample as well as its molecular structure. For example, NMR can quantitatively analyze mixtures containing known compounds. For unknown compounds, NMR can either be used to match against spectral libraries or to infer the basic structure directly. Once the basic structure is known, NMR can be used to determine molecular conformation in solution as well as studying physical properties at the molecular level such as conformational exchange, phase changes, solubility, and diffusion. In order to achieve the desired results, a variety of NMR techniques are available. The basics of NMR are described here.

You too can do NMR by using our NMR service.

The basis of NMR

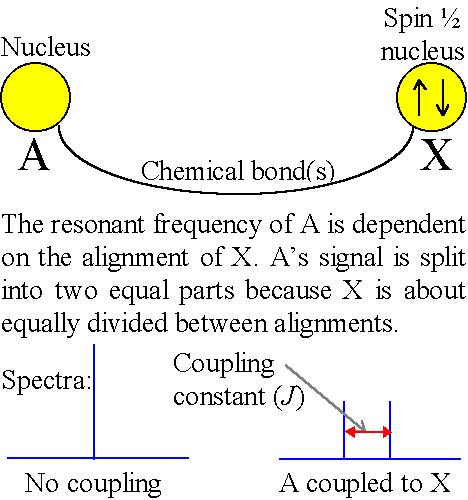
The principle behind NMR is that many nuclei have spin and all nuclei are electrically charged. If an external magnetic field is applied, an energy transfer is possible between the base energy to a higher energy level (generally a single energy gap). The energy transfer takes place at a wavelength that corresponds to radio frequencies and when the spin returns to its base level, energy is emitted at the same frequency. The signal that matches this transfer is measured in many ways and processed in order to yield an NMR spectrum for the nucleus concerned.

Fig. 1. The basis of NMR

Fig.1, above, relates to spin-½ nuclei that include the most commonly used NMR nucleus, proton (¹H or hydrogen-1) as well as many other nuclei such as ¹³C, ¹⁵N and ³¹P. Many nuclei such as deuterium (²H or hydrogen-2) have a higher spin and are therefore quadrupolar and although they yield NMR spectra, their energy diagram and some of their properties are different.

Chemical shift

The precise resonant frequency of the energy transition is dependent on the effective magnetic field at the nucleus. This field is affected by electron shielding which is in turn dependent on the chemical environment. As a result, information about the nucleus' chemical environment can be derived from its resonant frequency. In general, the more electronegative the nucleus is, the higher the resonant frequency. Other factors such as ring currents (anisotropy) and bond strain affect the frequency shift. It is customary to adopt tetramethylsilane (TMS) as the proton reference frequency. This is because the precise resonant frequency shift of each nucleus depends on the magnetic field used. The frequency is not easy to remember (for example, the frequency of benzene might be 400.132869 MHz) so it was decided to define chemical shift as follows to yield a more convenient number such as 7.17 ppm.

δ = (ν-ν₀)/ν₀

The chemical shift, using this equation, is not dependent on the magnetic field and it is convenient to express it in ppm where (for proton) TMS is set to ν₀ thereby giving it a chemical shift of zero. For other nuclei, ν₀ is defined as Ξ ν_TMS where Ξ (Greek letter Xsi) is the frequency ratio of the nucleus (e. g., 25.145020% for ¹³C).

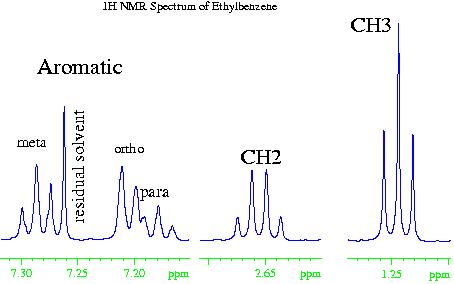
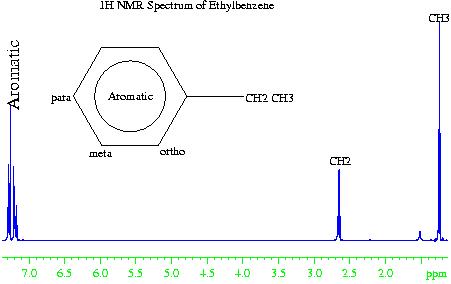
In the case of the ¹H NMR spectrum of ethyl benzene (fig. 2), the methyl (CH₃) group is the most electron withdrawing (electronegative) and therefore resonates at the lowest chemical shift. The aromatic phenyl group is the most electron donating (electropositive) so has the highest chemical shift. The methylene (CH₂) falls somewhere in the middle. However, if the chemical shift of the aromatics were due to electropositivity alone, then they would resonate between four and five ppm. The increased chemical shift is due to the delocalized ring current of the phenyl group.

Fig. 2. ¹H NMR spectrum of ethylbenznene

This definition of chemical shift is sufficient for most purposes. However, complications arise when comparing chemical shifts under different conditions: solvent, temperature, etc. Chemical shifts are affected slightly by isotopic substitution, an effect that is known as an isotope shift.

Spin-spin coupling

The effective magnetic field is also affected by the orientation of neighboring nuclei. This effect is known as spin-spin coupling (fig. 3) which can cause splitting of the signal for each type of nucleus into two or more lines.

Fig. 3. Spin-spin coupling

The size of the splitting (coupling constant or J) is independent of the magnetic field and is therefore measured as an absolute frequency (usually Hertz). The number of splittings indicates the number of chemically bonded nuclei in the vicinity of the observed nucleus. Some common coupling patterns are shown below (fig. 4). (Click here for more examples of common homonuclear coupling-patterns and for their use in assigning ¹H-NMR spectra as well as a description of heteronuclear coupling.)

Fig. 4. Examples of coupling patterns showing coupling constants

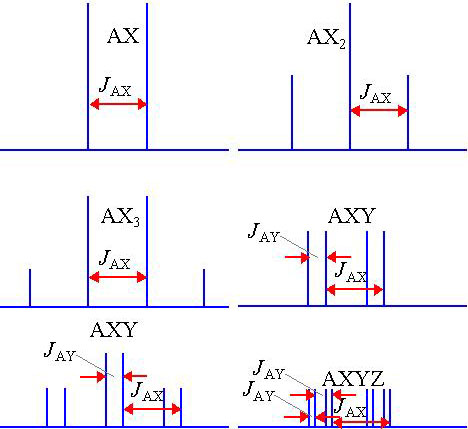
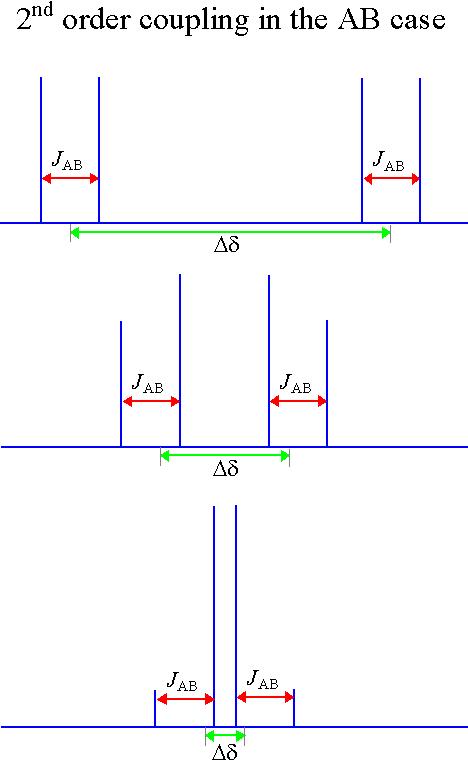
The above patterns are a first order approximation and are correct provided that all the coupled spins have widely separated chemical shifts. The different nuclei are labeled with the letters A and X (in a system of this type the letters come from widely separated parts of the alphabet). If the chemical shifts are similar then distortions in peak height occur as in the diagram below (the letters are also close together in the alphabet). For more than two spins, extra signals may appear. These effects are called second order coupling (fig. 5). Some examples are shown here and a detailed analysis of second order coupling is available in the literature.

Fig. 5. An example of second order coupling

Returning to the example of ethylbenzene (fig. 6), the methyl (CH₃) group has a coupling pattern in the form of A₃X₂, which to a first order approximation looks like an AX₂ multiplet. Likewise, the methylene (CH₂) group has the form A₂X₃ that is equivalent to AX₃. The first order approximation works because the groups are widely separated in the spectrum. The aromatic signals are close together and display second order effects. The ortho signal is a doublet AX while the meta and para signals are triplets.

Fig. 6. Couplings in the ethylbenzene spectrum