תמג של תהליכים דינמיים

השתמש בשירות התמ"ג שלנו למדוד תמ"ג דינמי.

תרמודינמיקה וקינטיקה של תגובות

תמ"ג דינמי היא ספקטרוסקופית התמ"ג של דוגמאות שעוברים שינויים פיזיים או כימיים עם הזמן. לדוגמה סיבוב סביב קשר כימי, היפוך טבעת, טאוטומריזם ערכיות וטאוטומריזם קטו-אנול. סקלות הזמנים שניתן למדידה פרוסות בין פיקושניות עד מאות שנים ואת השיטה שמשתמשים בה תלויה בסקלה של זמן. ניתן להשתמש בתמ"ג כדי לקבוע את שיווי המשקל ואת קבועי קצב התגובה שבם ניתן להשתמש כדי לחשב את הפרמטרים התרמודינמיים של המערכת.

כאן נדון רק בשיווי משקל בין שני מינים שהיא תופעה שכיחה למדי בספקטרום תמ"ג. עבור מערכות מורכבות יותר, יש לעיין בספרי הלימוד הרלוונטיים ומקורות אחרים.

אם ניתן שיווי משקל בין שני מינים A⇋B, קבוע שיווי משקל מוגדר כ- Keq=[A]/[B] . (ריכוז של המין הוא רשום בתוך סוגריים מרובעים [].)

אנרגיה חופשית, ΔG^⦵, של תגובה הוא כמות העבודה מכני שניתן להפיק מהתגובה. באנתלפיה ΔH^⦵, התגובה היא כמות החום שניתן להפיק מהתגובה. האנטרופיה, ΔS^⦵, של התגובה היא כמות האי סדר המיוצר על ידי תגובה, או ליֶתר דיוק, "את כמות האנרגיה התרמית שלא זמינה לעשות עבודה." האנרגיה החופשית התקנית, האנתלפיה והאנטרופיה קשורות לקבוע שיווי המשקל כדלקמן שבו R הוא קבוע הגז (8.3143 mol J K mol^-1 ו-T הוא טמפרטורה ב-K):

קבוע מהירות התגובה מוגדרת ע"י k=d[A]/([B]-[A])dt שבו t הוא הזמן. כאשר ניתן לעקוב ישירות אחר הריכוז כגון בחילוף איטי, ההבדל בריכוז הוא:

וקבועת המהירות היא:

האנרגיה החופשית של ההפעלה, ΔG^‡, קשורה ישירות לקבוע המהירות לפי המשוואה הבאה שבה k_B הוא קבוע בולצמן (1.381 × 10^-23 J K^-1) ו-h הוא קבוע פלנק (6.626 × 10^-34 J s).

ניתן לחשב את האנתלפיה ואת האנטרופיה של ההפעלה (ΔH^‡ ו-ΔS^‡, בהתאמה) מקבוע המהירות משתיים או יותר בטמפרטורות.

חילוף במהירות פחות ממילישנייה

תהליכים מהירים של פחות ממילישנייה הם ממוצעים לחלוטין בסקלת הזמן של תמ"ג (בסביבות שנייה) ונותנון ספקטרום רגילה שהוא ממוצע של המצבים המחליפים. עם זאת, למצבים בנפרד יש השפעה על ספקטרום התמ"ג. שיווי משקל החילוף הוא תלוי בטמפרטורה. אם לכל אחד מהמצבים המחליפים שי היסט כימי שונה (δ_A ו-δ_B) וההפרש באנתלפיה הסטנדרטית (ΔH^⦵) הוא דומה להבדל הנטרופיה הסטנדרטית (ΔS^⦵) כפול הטמפרטורה הוא נגיש, כלומר, ΔH^⦵ ≈ TΔS^⦵, אזי היסט הכימי ישתנה עם הטמפרטורה על פי המשוואות הבאות. אם ההיסט הכימי נמדד בטמפרטורות רבים, ניתן להתאיפם את הערכים של היסט הכימי של כל מצב, הפרש האנתלפיה וההבדל האנטרופיה לעקומה.

אם ניתן שיווי משקל A⇋B, היסט הכימי הממוצע, δ, ניתנת על ידי:

כאשר פותרים עבור רבוע שיווי משקל, מקבלים:

מדידת היסט כימי על פני טווח של טמפרטורה נותנת עקומת-S (תרשים 1) אם ΔH^⦵ = TΔS^⦵ איפשהו באמצע טווח הטמפרטורה. ניתן להסיק את הערכים של δ_A, δ_B, ΔH^⦵ ו-ΔS^⦵ באמצעות התאמה לא ליניארית לעקובה בצורת-S לפי המשוואה המורכבת למתה.

δ={exp[(TΔS-ΔH)/RT]δA+δB}/{1+exp[(TΔS-ΔH)/RT]}

תרשים 1. היסט כימי כפונקציה של הטמפרטורה של H2 של 9-פנילאנתרצן מונוסודיום מיונן בעמדה 9. בטמפרטורה נמוכה היא בזוג יונים מצומדים ובטמפרטורה גבוהה הוא זוג יונים מופרדים מסס.

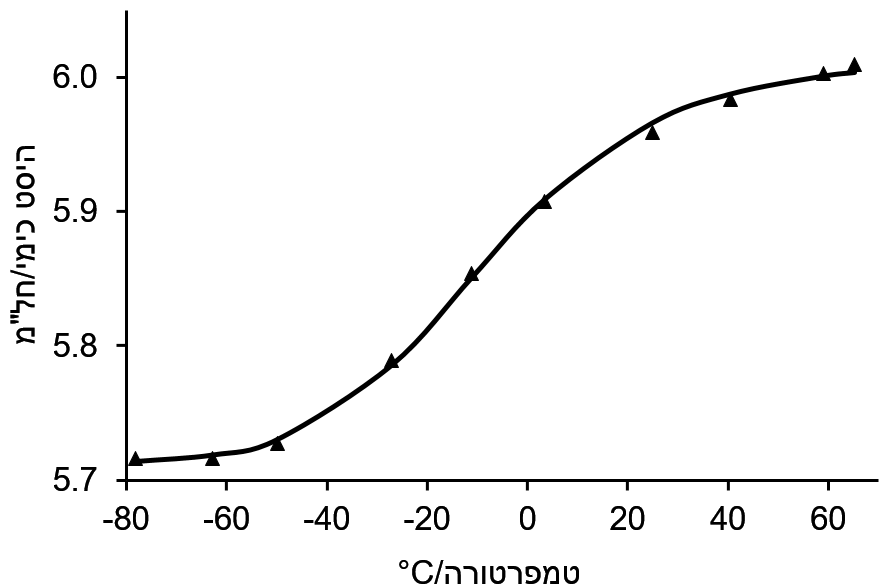
בדוגמה לעיל (תרשים 1), הערכים המותאמים הם כדלקמן: δ_A = חל"מ 5.71, δ_B = חל"מ 6.02, ΔH^⦵ = 32.6 mol kJ^-1 ו-ΔS^⦵ = 29.4 J mol^-1 K^-1. לחילופין, ניתן להשתמש בשיטה איטרטיבית פשוטה יותר כמפורט להלן.

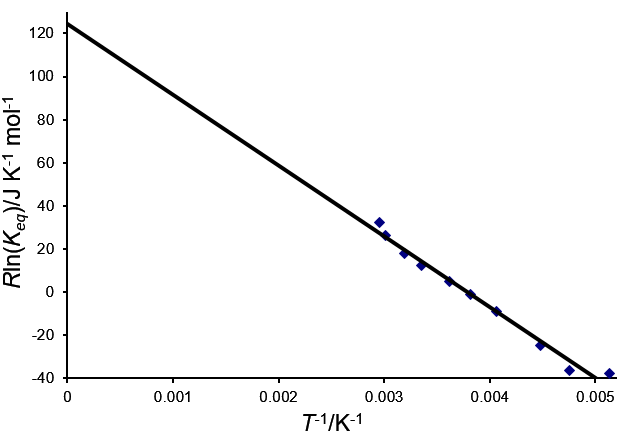
אם הטמפרטורה הנמוכה ביותר נמדדת מתאים ל-A טהור והטמפרטורה הגבוהה ביותר ל-B טהור, מכן ניתן לערוך Rln(K_eq) נגד 1/T (תרשים 2) שאמור לתת קו ישר שחותך עם ציר ה-y ב-ΔH^⦵ עם שיפוע של -ΔS^⦵. עם זאת, זה נדיר ואיטרציה נדרשת כמתואר במשוואות להלן.

תרשים 2. הערכה של Rln(K_eq) כנגד עבור H2 של מונוסודיום 9-פנילאנתרצן מיונן בעמדה 9. חותך את ציר ה-y ב-ΔH^⦵ עם שיפוע -ΔS^⦵.

חילוף בינוני-מהיר, מילישניות עד שניות

תרשים 3. ספקטרומי חילוף דינמי של תיאוריאה אצטט ב-DMSO-d₆

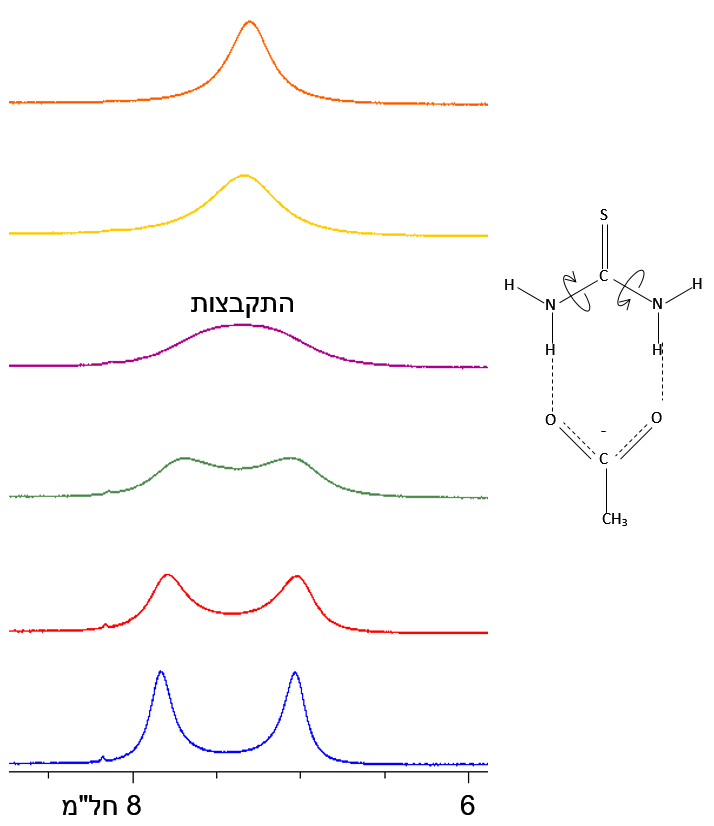
חילוף בינוני-מהיר (מאלפית השנייה עד לשנייה) גורם להתרחבות ופיצול הקו. לדוגמה, תרשים 3 מציג את הספקטרום של תיאוריאה אצטט. במצב של חילוף מהיר (בדרך כלל בטמפרטורה גבוה), הסיגנלים הנובעים משני הגרעינים המתחלפים מתמזגים לאחד. בקצה הטווח המהיר הספקטרום מראה סיגנל יחיד מורחב. הדוגמה לעיל הוא מקרה פשוט של שני סינגלטים בואתו עוצמה שמתחלפים (כלומר, ΔG^⦵ = 0 ו-K_eq = 1). רוחב הקו (בחצי הגובה), w_½ בהרץ, עבור חילוף יחסית מהר, הוא Δν/k+1/piT2* שבה Δν הוא הפרש בתדר התהודה בין המינים בהרץ, k הוא קבוע המהירות ב-s^-1 ו-T₂^* הוא שיעור הפיזור או רלקסציה הרוחבי בפועל בשניות. כאשר החילוף מאט עם קירור קיימת סטייה בערך והספקטרום מתפצל שנים כאשר Δν/k=2.22 שנקרא נקודת ההתקבצות. כאשר החילוף מאט עוד יותר, הספקטרום מתחיל שוב להתחדד עם רוחב קו שמקרב ל- k+1/piT2* ושני סיגנלים חדים מופיעים כאשר החילוף איטי. ניתן לקבוע את קבוע המהירות מנקודת ההתקבצות או בנקודת במרחק סבירה מנקודת ההתקבצות באמצעות המשוואות הבאות.

k עבור חילוף מהיר עבור חילוף מהיר

k בהתמזגות בהתקבצות

k עבור חילוף אטי עבור חילוף אטי

שינוי הטמפרטורה משנה את קבוע מהירות החילוף ומאפשר קביעת הקבועים התרמודינמיים של מצב המעבר. ייתכן שבטמפרטורות נמוכות, קבוע מהירות החילוף הוא מספיק איטי כדי ש- linewidth equation מאפשר את מדידת T₂^*. בטמפרטורות גבוהות, החילוף הוא מהיר יותר וניתן די מהר ש-. באופן אידיאלי, נקודת התקבצות אמור להיות בטמפרטורה נגישה.

תרשים 4. מהירות החילוף של תיאוריאה אצטט סיבוב קשר ה-C-N ב-DMSO-d₆

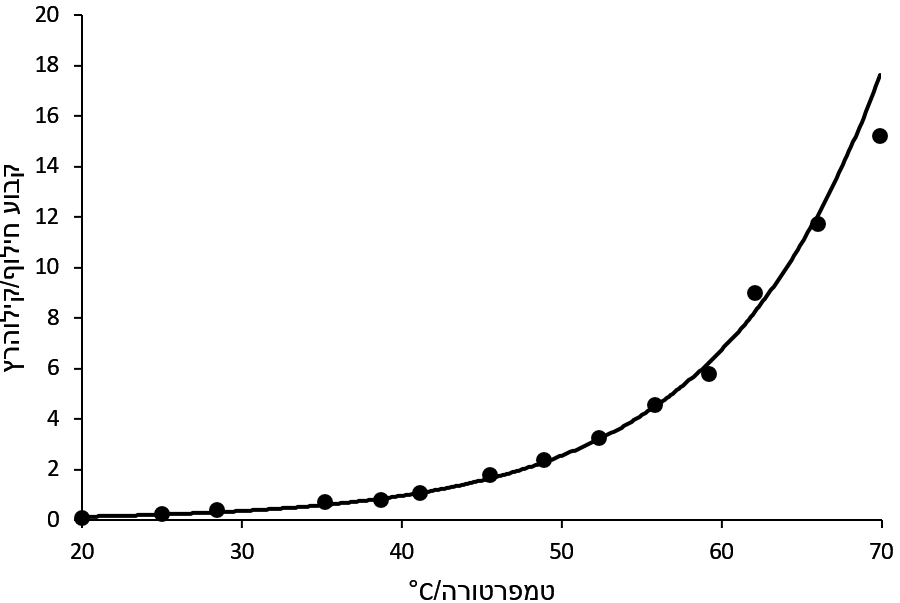
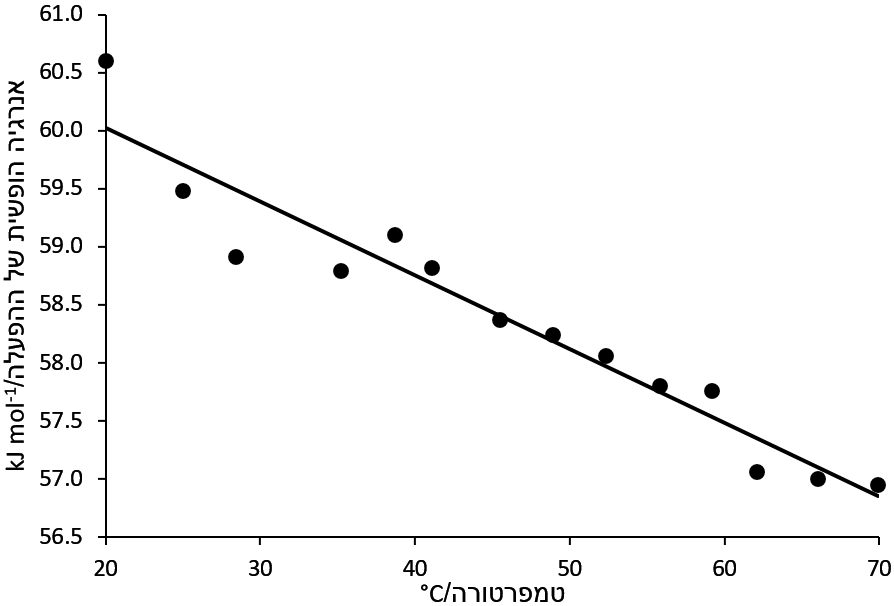
קבוע החילוף גדל בצורה מערוכתי עם טמפרטורה (תרשים 4). האנרגיה החופשי פוחת קצת עם חימום (תרשים 5). בדוגמה הזאת, ΔH^‡ בערך 79 kJ mol^-1 ו-ΔS^‡ הוא 63 J mol^-1 K^-1.

תרשים 5. אנרגיה החופשים של מצב המעבר של תיאוריאה אצטט סיבוב קשר ה-C-N ב-DMSO-d₆

חילוף בינוני-איטי, שניות עד דקות

חילוף בינוני-איטי (עד בערך דקה) נותן סיגנלים חדות ונפרדות אלא גם נותן סיגנלי הצלבה של חילוף בספקטרום EXSY/NOESY. אם משתמשים בזמני ערבוב קטנים והשהיות רלקסציה ארוכות, הספקטרום EXSY/NOESY הוא כמותיות והתוצאות בטמפרטורות שונוה יכולות לתת את הפרמטרים התרמודינמיים של מצב המעבר כמו במקרה של חילוף במהירות בינוני-מהיר. הריכוזים היחסיים נותנים לקבוע את תכונות תרמודינמיות של שיווי המשקל. לחילוף פשוט בין שני סיגנלים שווים האינטגרל של סיגנל ההצלבה, [AB], קשור לאינטגרל סיגנל האלכסון, [AA], כדלקמן וניתן להשתמש בו כדי לקבוע את קבוע המהירות, שבו τ הוא זמן הערבוב.

אם הסיגנל המצולב הוא קטן ביחס סיגנל האלכסון, הערך של k הוא קטן והמשוואה לעיל מתקרב ליחס ליניארי למתה שניתן לפתור עבור k.

כאשר יש יותר משני מינים מתחלפים, ניתן להשתמש במשוואה הלינארית לעיל רק כאשר סיגנלי ההצלבה קטנות. כאשר סיגנלי ההצלבה יותר גדולים נדרש ניתוח איטרטיבי של מטריצה.

חילוף איטי, יותר ממספר דקות

לחילוף איטי (מעל דקה) אפשר להתחיל בתערובת שאינה בשיווי משקל ולבחון את השינוי הריכוז של כל מין לאורך זמן בטמפרטורה קבועה. זה מספיק כדי לקבוע את ההבדל באנרגיה חופשית וניתן לחזור בטמפרטורות שונות, במטרה לקבל את ההבדל באנתלפיה והאנטרופיה. אם החילוף איטי מדי כדי למדוד בטמפרטורת החדר ניתן לחמם את הדוגמה. ככלל אצבע, מהירות התגובה מוכפל עם כל חימום של ‎10°C‏ למרות שהערך המדויק תלוי באנטרופיה של מצב המעבר. לכן תגובה שלוקח שעה (k = 0.00028) ב-‎160°C‏ עלול לקחת סדר גודל של שנה בטמפרטורת החדר. עבור תגובות אפילו איטיות יותר, ניתן להשאיר את תערובת התגובה בתנור במשך מספר שבועות ולאחר מכן למדד אותה על ידי תמ"ג. ניסויים כאלה יכולים לקבוע את סדר הגודל הצפוי של אריכות חיים של מאות שנים עבור חומרים. אם מדידות כאלה נעשות בשניים או יותר טמפרטורות, אז ניתן למדוד את האנטרופיה של ההפעלה שמוביל למהירות תגובה מדויקת יותר בטמפרטורת החדר.

מקורות

Dynamic NMR spectroscopy, Eds. P. Dhiel, E, Fluck, R. Kosfeld, NMR Basic Principles and Progress series vol. 15, Springer-Verlag Berlin 1982.
G. E. Hawkes, L. Y. Lian, E. W. Randall, K. D. Sales, Two-dimensional nuclear magnetic resonance for the quantitative analysis of three-site exchange in the ruthenium cluster [Ru₃(mu-H)(CO)₉(MeCCHCMe)] J. Magn. Reson, 65, 173-177 (1985)
A. D. Bain, Chemical exchange in NMR, Prog. Nuc. Magn. Reson. Spectrosc., 43, 63-103 (2003).
I. Bányai, Dynamic NMR for coodination chemistry, New. J. Chem., 42, 7569-7581 (2018).

תמ"ג של תהליכים דינמיים